La anatomía de un problema de optimización lineal

La optimización lineal es mucho más que una herramienta para resolver problemas prácticos de producción, logística o asignación de recursos: también constituye un objeto profundamente elegante desde el punto de vista teórico.

Detrás de cada solución óptima se esconden estructuras geométricas y algebraicas que nos permiten comprender:

cuándo existen soluciones óptimas,
cómo se alcanzan,
y de qué manera puede describirse el conjunto completo de soluciones factibles.

Este post explora los conceptos fundamentales que sustentan la teoría de la optimización lineal:

los puntos extremos,
las direcciones extremas,
cómo caracterizarlos,
y el teorema de representación para el conjunto de soluciones factibles.

El objetivo es proporcionar un marco conceptual claro que ayude a entender el por qué detrás de algoritmos como el Símplex, más allá del simple cálculo mecánico de una solución óptima. En optimización lineal, lo verdaderamente interesante no es solo encontrar el óptimo, sino comprender la geometría que hay detrás.

Notación y definiciones

El problema de optimización lineal en su forma estándar se escribe como:

\[\begin{aligned} \min \;\; & z = \mathbf{c}^\intercal \mathbf{x} \\ \text{s.a:}\;\; & \mathbf{A}\mathbf{x} = \mathbf{b} \\ & \mathbf{x} \geqslant \mathbf{0}. \end{aligned}\]

El conjunto de soluciones factibles se define como:

\[\mathcal{S}=\{\mathbf{x} \in \mathbb{R}^n : \mathbf{A}\mathbf{x} = \mathbf{b},\; \mathbf{x}\geqslant \mathbf{0}\}.\]

La matriz de coeficientes técnicos $\mathbf{A}\in\mathbb{R}^{m\times n}$ puede interpretarse como un conjunto de $n$ vectores en $\mathbb{R}^m$:

\[\mathbf{A} = (\mathbf{a}_1,\ldots,\mathbf{a}_n),\]

donde cada columna es:

\[\mathbf{a}_j = \begin{pmatrix} a_{1j} \\ a_{2j} \\ \vdots \\ a_{mj} \end{pmatrix}, \qquad j=1,\ldots,n.\]

Bases y soluciones básicas

Un supuesto habitual en la teoría es que la matriz $\mathbf{A}$ tiene rango máximo:

\[\mathrm{rg}(\mathbf{A}) = m.\]

En ese caso, existe al menos una submatriz cuadrada

\[\mathbf{B}\in\mathbb{R}^{m\times m}, |\mathbf{B}| \neq 0.\]

llamada base.

Los $m$ vectores columna que forman la base $\mathbf{B}$ son linealmente independientes.

Elegir una base permite descomponer la matriz como:

\[\mathbf{A} = (\mathbf{B},\mathbf{N}),\]

lo que induce una partición natural del vector solución:

\[\mathbf{x} = \begin{pmatrix} \mathbf{x}_{\mathbf{B}} \\ \mathbf{x}_{\mathbf{N}} \end{pmatrix},\]

donde:

$\mathbf{x}_{\mathbf{B}}\in\mathbb{R}^m$ son las variables básicas,
$\mathbf{x}_{\mathbf{N}}\in\mathbb{R}^{n-m}$ son las variables no básicas.

Solución básica

Se dice que $\mathbf{x}\in\mathbb{R}^n$ es una solución básica si existe una base $\mathbf{B}\subset\mathbf{A}$ tal que las variables no básicas son cero:
\[\mathbf{x} = \begin{pmatrix} \mathbf{B}^{-1}\mathbf{b} \\ \mathbf{0} \end{pmatrix}.\]

Solución básica factible

Una solución básica se dice factible si además satisface la condición de no negatividad:
\[\mathbf{B}^{-1}\mathbf{b}\geqslant 0.\]

Las soluciones básicas factibles son especialmente importantes porque están directamente relacionadas con los puntos extremos de la región factible, como veremos en las siguientes secciones.

Convexidad

Uno de los aspectos más profundos detrás del análisis teórico de la optimización lineal es la convexidad.

Un conjunto no vacío $\mathcal{C} \subset \mathbb{R}^n$ se dice que es convexo si:
\[\lambda \mathbf{x} + (1-\lambda)\mathbf{y} \in \mathcal{C} \qquad \forall \mathbf{x},\mathbf{y}\in\mathcal{C},\; \forall \lambda\in[0,1].\]

Geométricamente, esto significa que dados dos puntos cualesquiera del conjunto, el segmento que los une permanece completamente dentro del conjunto.

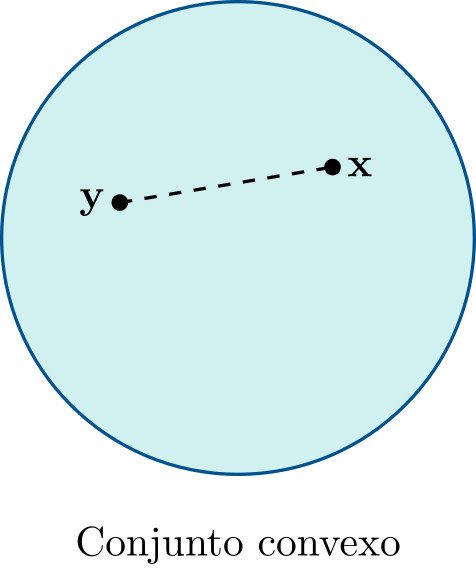
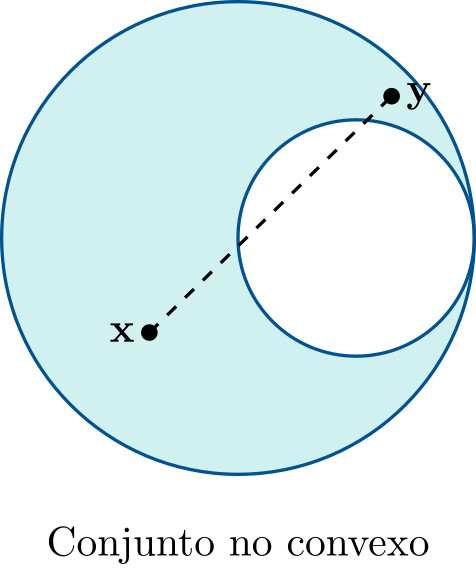
El conjunto de soluciones factibles de un problema de optimización lineal,
\[\mathcal{S}=\{\mathbf{x}\in\mathbb{R}^n:\mathbf{A}\mathbf{x}=\mathbf{b},\;\mathbf{x}\geqslant 0\},\]
es un conjunto convexo.

Puntos extremos

Aunque $\mathcal{S}$ contiene infinitos puntos, su estructura está determinada por un conjunto más pequeño de elementos especiales: los puntos extremos, que representan los “vértices” del politopo factible.

Si existe una solución óptima, entonces puede encontrarse en un punto extremo.

Por tanto, es importante entender qué son los puntos extremos y cómo caracterizarlos.

Dado un conjunto convexo $\mathcal{C}\subset\mathbb{R}^n$, un punto $\mathbf{x}\in\mathcal{C}$ se dice punto extremo si:
\[\mathbf{x}=\lambda\mathbf{y}+(1-\lambda)\mathbf{z}, \;0<\lambda<1, \;\mathbf{y},\mathbf{z}\in\mathcal{C} \Rightarrow\] \[\mathbf{x}=\mathbf{y}=\mathbf{z}.\]

Es decir, un punto extremo no puede escribirse como combinación convexa de otros dos puntos distintos del conjunto.

Caracterización de puntos extremos

Sea $\mathcal{S}=\{\mathbf{x}\in\mathbb{R}^n:\mathbf{A}\mathbf{x}=\mathbf{b},\;\mathbf{x}\geqslant 0\},$ donde $\mathbf{A}\in\mathbb{R}^{m\times n}$ y $\mathrm{rg}(\mathbf{A})=m$. Entonces:

$\bar{\mathbf{x}}$ es punto extremo de $\mathcal{S}$ si y sólo si

$\exists\,\mathbf{B}\subset\mathbf{A}$ tal que $|\mathbf{B}|\neq 0, \;\mathbf{B}^{-1}\mathbf{b}\geqslant 0.$

En cuyo caso:
\[\bar{\mathbf{x}}= \begin{pmatrix} \mathbf{B}^{-1}\mathbf{b}\\ \mathbf{0} \end{pmatrix}.\]

El número de puntos extremos está acotado por:

\[\binom{n}{m}.\]

Si $\mathcal{S} \neq \emptyset$, existe al menos un punto extremo.

Direcciones extremas

En problemas con regiones factibles no acotadas aparecen las direcciones extremas, que describen cómo el conjunto puede extenderse hacia el infinito.

Un vector $\mathbf{d}\neq 0$ es una dirección de un conjunto convexo $\mathcal{C}$ si:
\[\forall\mathbf{x}\in\mathcal{C},\; \forall\mu\geqslant 0 \Rightarrow \mathbf{x}+\mu\mathbf{d}\in\mathcal{C}.\]
Dos direcciones $\mathbf{d}^1$ y $\mathbf{d}^2$ son equivalentes si $\mathbf{d}^1=\alpha\mathbf{d}^2,\; \alpha>0.$

En el problema de optimización lineal,

Dado el conjunto de soluciones factibles de un problema de optimización lineal, $\mathcal{S}={\mathbf{x} \in \mathbb{R}^n : \mathbf{A}\mathbf{x} = \mathbf{b}, \mathbf{x} \geqslant \mathbf{0}}$ entonces,

$\mathbf{d}$ es dirección de $\mathcal{S}$ si y sólo si $\mathbf{d} \geqslant \mathbf{0}, \; \mathbf{d} \neq \mathbf{0}$ y $\mathbf{A}\mathbf{d} = \mathbf{0}$

Dado un conjunto convexo $\mathcal{C} \subset \mathbb{R}^n$, una dirección $\mathbf{d} \in \mathbb{R}^n$ es una dirección extrema en $\mathcal{C}$ si, cuando se expresa como:
\[\mathbf{d} = \mu_1 \mathbf{d}^1 + \mu_2 \mathbf{d}^2\]
donde $\mu_1,\mu_2 > 0$ y $\mathbf{d}^1,\mathbf{d}^2$ son direcciones de $\mathcal{C}$, se concluye que las tres direcciones son necesariamente equivalentes:
\[\mathbf{d} \simeq \mathbf{d}^1 \simeq \mathbf{d}^2\]

Las direcciones extremas también se pueden caracterizar.

Caracterización de direcciones extremas

Dado $\mathcal{S}={\mathbf{x} \in \mathbb{R}^n : \mathbf{A}\mathbf{x} = \mathbf{b}, \mathbf{x} \geqslant \mathbf{0}}$, donde $\mathbf{A}$ es una matriz $m \times n$ y $\mathrm{rg}(\mathbf{A}) = m,$ entonces:

$\mathbf{d}$ es una dirección extrema de $\mathcal{S}$ si y sólo si $\exists \mathbf{B} \subset \mathbf{A},$ donde $|\mathbf{B}| \neq 0$ tal que $\mathbf{A}=(\mathbf{B},\mathbf{N})$ y, existe un vector columna $\mathbf{a}_j \in \mathbf{N}$ que cumple $\mathbf{B}^{-1}\mathbf{a}_j \leqslant \mathbf{0}$ de modo que $\mathbf{d}=\alpha\mathbf{d}^0,$ donde $\alpha > 0$ y $\mathbf{d}^0 = \begin{pmatrix}-\mathbf{B}^{-1} \mathbf{a}_j \ \mathbf{e}_j\end{pmatrix}$.

$\mathbf{e}_j$ es un vector cuyas componentes son todas nulas excepto la $j$-ésima que toma valor 1.

El número de direcciones extremas está acotado por:

\[\binom{n}{m+1}.\]

Teorema de Representación

El teorema de representación es la consecuencia de un conjunto de teoremas de representación gracias a los trabajos de Minkowski, Carathéodory, Steinitz, Weyl and Motzkin ((Minkowski, 1897), (Carathéodory, 1907), (Steinitz, 1916), (Weyl, 1935) y (Motzkin, 1936)) para conjuntos convexos que se demostraron con anterioridad al nacimiento de la optimización lineal.

Teorema de Representación

Dado el conjunto de soluciones factibles del problema de optimización lineal $\mathcal{S}={\mathbf{x} \in \mathbb{R}^n : \mathbf{A}\mathbf{x} = \mathbf{b}, \mathbf{x} \geqslant \mathbf{0}}$, donde $\mathbf{A}$ es una matriz $m \times n$ y $\mathrm{rg}(\mathbf{A}) = m$, sea ${\mathbf{x}^1,\ldots,\mathbf{x}^k}$ el conjunto de puntos extremos de $\mathcal{S}$ y sea ${\mathbf{d}^1,\ldots,\mathbf{d}^l}$ el conjunto de sus direcciones extremas, entonces se verifica que:
\[\mathbf{x} \in \mathcal{S} \Leftrightarrow \wedge \begin{cases} \exists (\lambda_1,\ldots,\lambda_k) & \lambda_i \geqslant 0, \; \forall i=1,\ldots,k : \displaystyle \sum_{i=1}^k \lambda_i = 1 \\ \exists (\mu_1,\ldots,\mu_l) & \mu_j \geqslant 0, \; \forall j=1,\ldots,l\end{cases}\]
de modo que:
\[\mathbf{x} = \sum_{i=1}^k \lambda_i \mathbf{x}^i + \sum_{j=1}^l \mu_j \mathbf{d}^j\]

Este teorema permite definir cualquier solución del problema de optimización lineal en función de sus puntos extremos y direcciones extremas. Para ello, es necesario proporcionar estos dos conjuntos, usando los teoremas de caracterización presentados anteriormente.

Ejemplos

Sea el conjunto de soluciones factibles (independiente de la función objetivo) de un problema de optimización lineal y su formulación estándar (añadiendo variables de holgura):

\[\begin{aligned} -x_1 + x_2 & \leqslant 2 \\ x_1 - 2x_2 & \leqslant 2 \\ x_1, x_2 & \geqslant 0 \end{aligned} \qquad \begin{aligned} -x_1 + x_2 + x_3^h & = 2 \\ x_1 - 2x_2 + x_4^h & = 2 \\ x_1, x_2, x_3^h, x_4^h & \geqslant 0 \end{aligned}\]

Este problema tiene un total de 3 puntos extremos:

\[\mathbf{x}_1 = \begin{pmatrix}0 \\ 0 \\ 2 \\ 2\end{pmatrix} \qquad \mathbf{x}_2 = \begin{pmatrix}2 \\ 0 \\ 4 \\ 0\end{pmatrix} \qquad \mathbf{x}_3 = \begin{pmatrix}0 \\ 2 \\ 0 \\ 6\end{pmatrix}\]

y dos direcciones extremas:

\[\mathbf{d}_1 = \begin{pmatrix}1 \\ 1 \\ 0 \\ 1\end{pmatrix} \qquad \mathbf{d}_2 = \begin{pmatrix}2 \\ 1 \\ 1 \\ 0\end{pmatrix}\]

que se representan en la siguiente figura, en $\mathbb{R}^2$:

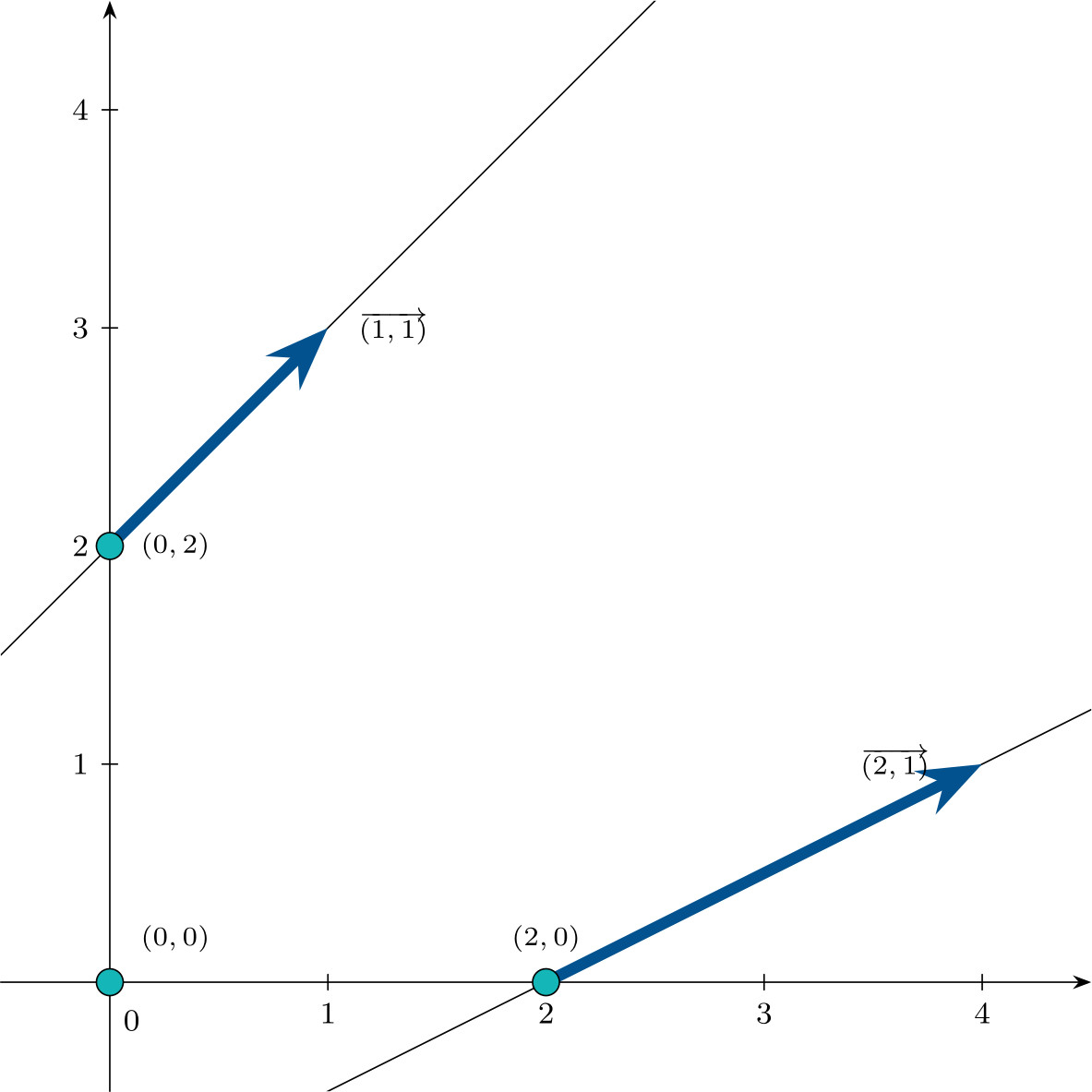
Usando el teorema de representación, el conjunto $\mathcal{S}$ se puede expresar:

\[\begin{aligned} \mathcal{S} =\Biggl\{ &\lambda_1 \begin{pmatrix} 0\\0\\2\\2 \end{pmatrix} +\lambda_2 \begin{pmatrix} 2\\0\\4\\0 \end{pmatrix} +\lambda_3 \begin{pmatrix} 0\\2\\0\\6 \end{pmatrix} +\mu_1 \begin{pmatrix} 1\\1\\0\\1 \end{pmatrix} +\mu_2 \begin{pmatrix} 2\\1\\1\\0 \end{pmatrix} : \\[0.4em] & \lambda_1+\lambda_2+\lambda_3=1, \lambda_1,\lambda_2,\lambda_3\geqslant 0, \qquad \mu_1,\mu_2\geqslant 0 \Biggr\}. \end{aligned}\]

Consecuencias del teorema de representación

El teorema de representación permite categorizar los distintos tipos de soluciones del problema de optimización lineal de minimización.

Solución óptima no acotada si existe dirección extrema $\mathbf{d}^j$ con $\mathbf{c}^\intercal \mathbf{d}^j < 0$.
Solución óptima si todas las direcciones extremas cumplen $\mathbf{c}^\intercal \mathbf{d}^j \geqslant 0$ o no existen direcciones extremas, alcanzándose en un punto extremo.

Procedimiento de resolución y combinatoria

En el conjunto de restricciones mostrado anteriormente, se analizarán diferentes vectores de coste que proporcionan diferentes funciones objetivo y, por tanto, diferentes tipos de solución final.

$\mathbf{c}^\intercal = (2,-3,0,0)$

$\mathbf{c}^\intercal \mathbf{d}^1 = (2,-3,0,0)\begin{pmatrix}1 \\ 1 \\ 0 \\ 1\end{pmatrix} = -1 < 0$, el problema tiene solución óptima no acotada.

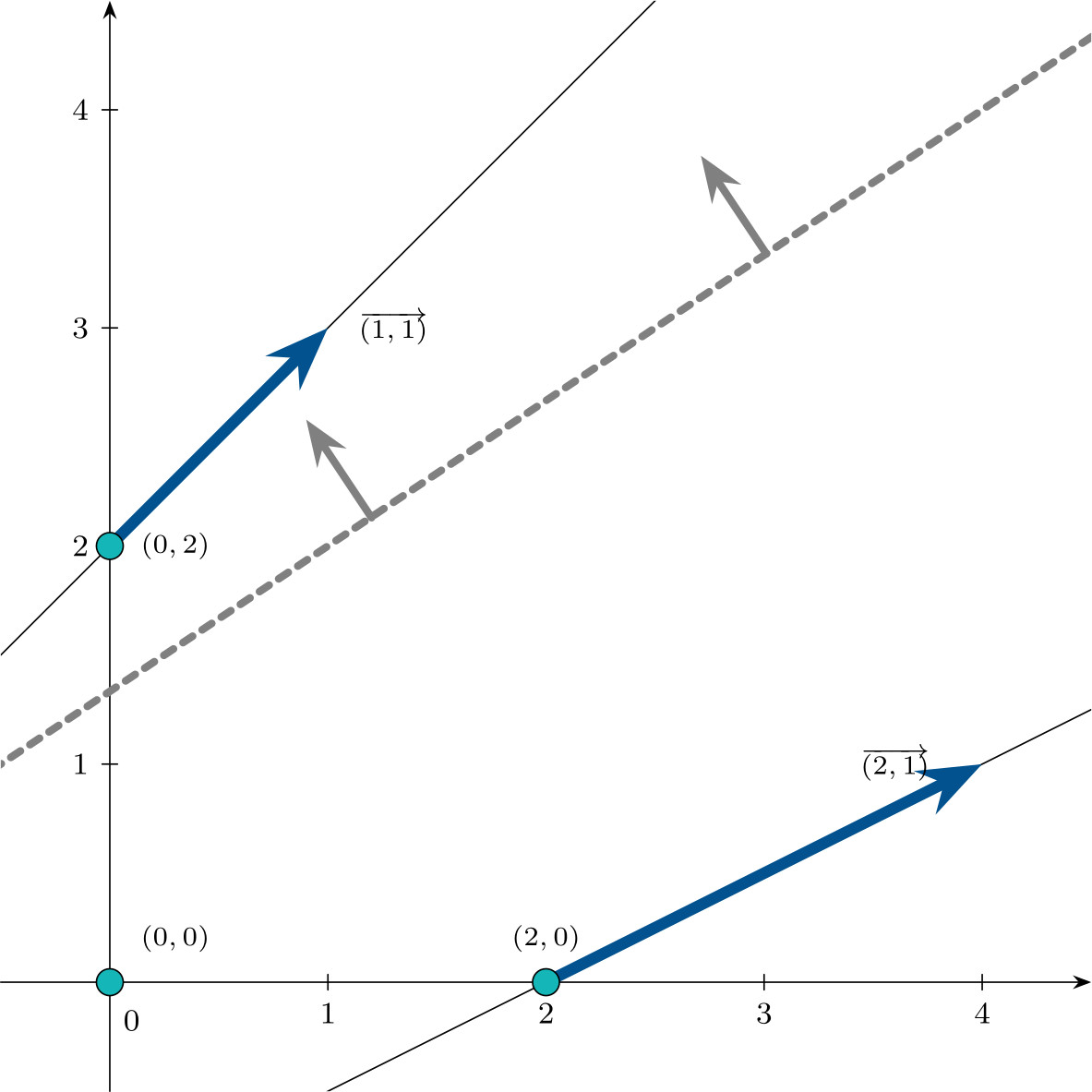
$\mathbf{c}^\intercal = (4,-3,0,0)$

$\mathbf{c}^\intercal \mathbf{d}^1 \geqslant 0$ y $\mathbf{c}^\intercal \mathbf{d}^2 \geqslant 0$ el problema tiene solución óptima y se alcanza en el vértice cuyo valor en la función objetivo es mínimo, es decir, en $\mathbf{x}^3$ ($\mathbf{c}^\intercal \mathbf{x}^3 = -6$).

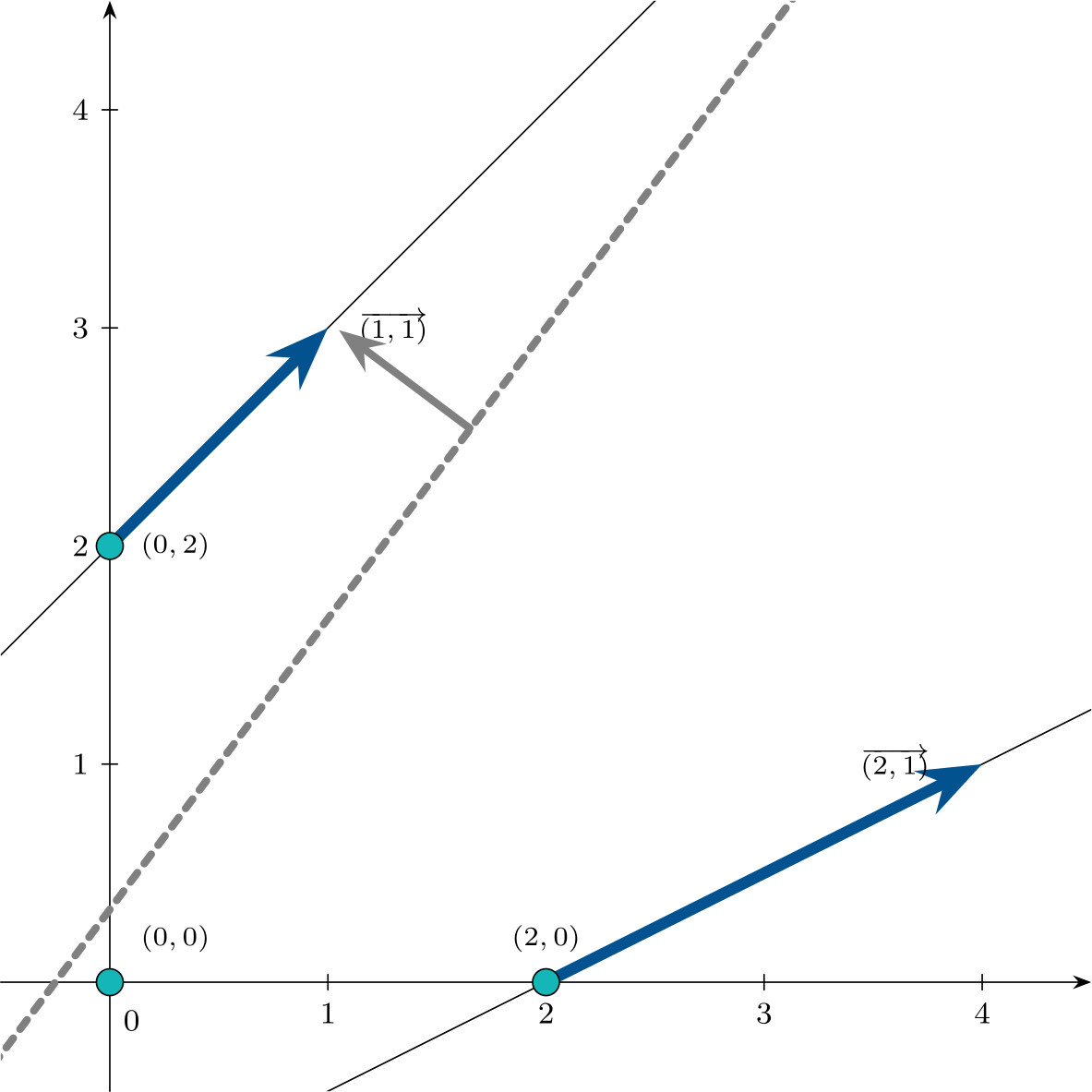
$\mathbf{c}^\intercal = (0,1,0,0)$

$\mathbf{c}^\intercal \mathbf{d}^1 \geqslant 0$ y $\mathbf{c}^\intercal \mathbf{d}^2 \geqslant 0$ el problema tiene solución óptima y se alcanza en el vértice cuyo valor en la función objetivo es mínimo. En este caso, hay dos vértices que alcanzan el valor mínimo, $\mathbf{x}^1$ y $\mathbf{x}^2$, donde $\mathbf{c}^\intercal \mathbf{x}^1 = \mathbf{c}^\intercal \mathbf{x}^2 = 0$.

El conjunto de soluciones óptimas del problema viene dado por:

\[\left\{\lambda\begin{pmatrix}0 \\ 0 \\ 2 \\ 2\end{pmatrix} + (1-\lambda)\begin{pmatrix}2 \\ 0 \\ 4 \\ 0\end{pmatrix}, \;\; \lambda \in [0,1]\right\}\]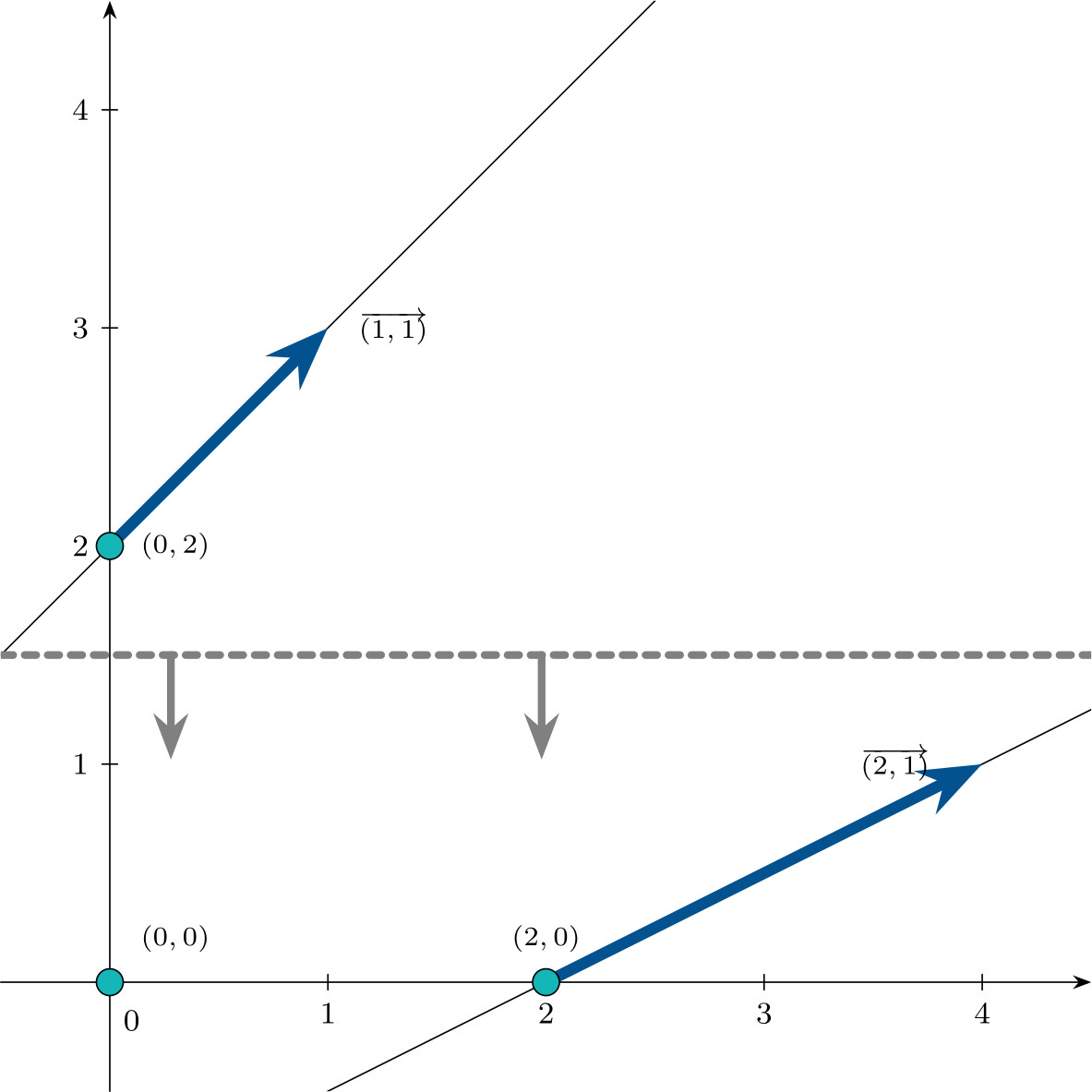

$\mathbf{c}^\intercal = (1,-1,0,0)$

$\mathbf{c}^\intercal \mathbf{d}^1 \geqslant 0$ y $\mathbf{c}^\intercal \mathbf{d}^2 \geqslant 0$, observándose que $\mathbf{c}^\intercal \mathbf{d}^1 \geqslant 0$, el problema tiene solución óptima. En este caso, evaluando los vértices, el valor mínimo se alcanza en $\mathbf{x}^3$, donde $\mathbf{c}^\intercal \mathbf{x}^3 = -2$.

El conjunto de soluciones óptimas del problema viene dado por:

\[\left\{\begin{pmatrix}0 \\ 2 \\ 0 \\ 6\end{pmatrix} + \mu\begin{pmatrix}1 \\ 1 \\ 0 \\ 1\end{pmatrix}, \;\; \mu \geqslant 0 \right\}\]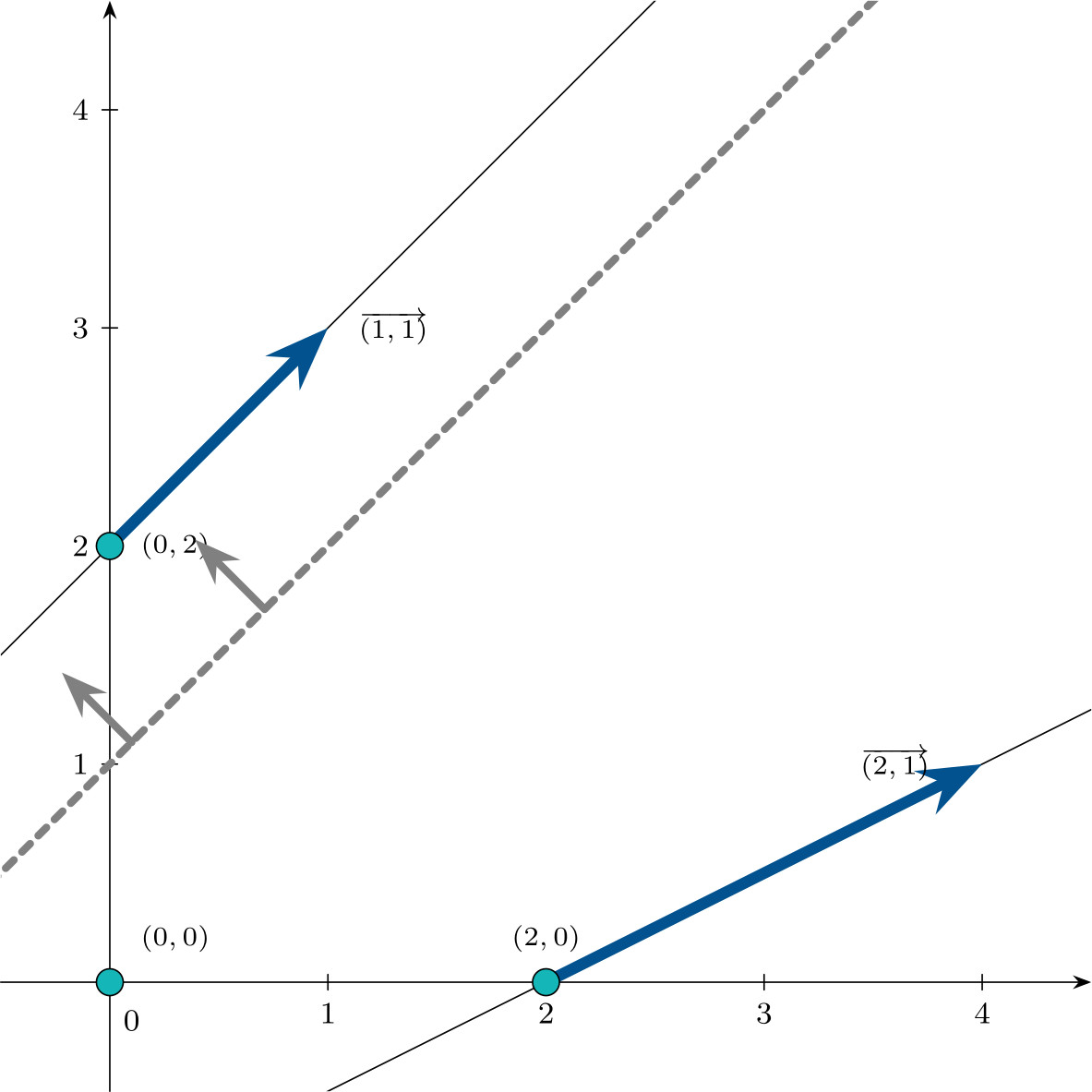

Múltiples soluciones en región no acotada

Combinatoria

El análisis combinatorio de todas las bases crece muy rápido. Para un problema de pequeñas dimensiones, por ejemplo $n=40$ y $m=20$:

\[\binom{40}{20}=137.846.528.820\]

Aunque el procedimiento de enumerar todos los puntos extremos y direcciones extremas no es práctico para problemas de gran tamaño debido al crecimiento combinatorio, este análisis proporciona los elementos teóricos fundamentales: nos permite comprender la estructura geométrica de la región factible, caracterizar los tipos de soluciones posibles y sentar las bases para el desarrollo de algoritmos eficientes, como el Símplex, que explotan precisamente estas propiedades.